Pembahasan Matematika Dasar No. 51 - 55 TKPA SBMPTN 2016 Kode Naskah 321

Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2016 kode naskah 321 nomor 51 sampai dengan nomor 55 tentang:

• kaidah pencacahan, permutasi, dan kombinasi, 
• komposisi fungsi, 
• invers fungsi, 
• matriks, serta 
• barisan dan deret.

Soal No. 51 tentang Kaidah Pencacahan, Permutasi, dan Kombinasi

Tujuh finalis lomba menyanyi tingkat SMA di suatu kota berasal dari 6 SMA yang berbeda terdiri atas empat pria dan tiga Wanita. Diketahui satu pria dan satu wanita berasal dari SMA “A”. Jika urutan tampil diatur bergantian antara pria dan wanita, serta finalis dari SMA “A” tidak tampil berurutan maka susunan urutan tampil yang mungkin ada sebanyak ….A.   144
B.   108
C.   72
D.   36
E.   35

Pembahasan

Misalkan:

P    : finalis pria
W   : finalis wanita
P_A   : finalis pria dari SMA “A”
W_A : finalis wanita dari SMA “A”

Finalis pria dan wanita tampil bergantian serta finalis dari SMA “A” tidak tampil berurutan. Susunan yang mungkin adalah:

1. P_A W P W_A P W P
2. P_A W P W P W_A P
3. P W P_A W P W_A P
4. P W_A P W P_A W P
5. P W_A P W P W P_A
6. P W P W_A P W P_A

Sekarang perhatikan salah satu susunan tersebut, misal susunan yang pertama.

P_A W P W_A P W P

Dengan P_A dan W_A pada posisi yang tetap, 3 P dan 2 W bisa dipertukarkan. Sehingga banyak urutan yang mungkin adalah:

3! × 2! = 3 × 2 × 1 × 2 × 1
            = 12

Demikian juga dengan 5 susunan yang lain dapat diberlakukan seperti di atas. Sehingga banyak seluruh urutan susunan adalah:

6 × 12 = 72

Jadi, susunan urutan tampil yang mungkin ada sebanyak 72 (C).

Soal No. 52 tentang Komposisi Fungsi

Diberikan fungsi f(x) = ax − b dan g(x) = cx + b dengan a, b, dan c adalah bilangan-bilangan real positif. Syarat agar f(g(x)) > g(f(x)) adalah ….

A.   a + c > 1
B.   a + c > b
C.   a + c > 2
D.   a + c > 2b
E.   a + c > 4

Pembahasan

f(g(x)) berarti menggantikan x pada fungsi f dengan g(x).

          f(g(x)) > g(f(x))
     a g(x) − b > c f(x) + b
a(cx + b) − b > c(ax − b) + b
 acx + ab − b > acx − bc + b

acx pada ruas kiri dan kanan bisa dicoret. Sementara itu sisa suku yang lain masing-masing dibagi b. Diperoleh:

a − 1 > −c + 1
 a + c > 2

Jadi, syarat agar f(g(x)) > g(f(x)) adalah a + c > 2 (C).

Soal No. 53 tentang Invers Fungsi

Jika fungsi f dan g mempunyai invers dan memenuhi f(2x) = g(x − 3) maka f⁻¹(x) = ….

A.   g⁻¹(x/2 − 2/3)
B.   g⁻¹(x/2) − 2/3
C.   g⁻¹(2x + 6)
D.   2g⁻¹(x) − 6
E.   2g⁻¹(x) + 6

Pembahasan

Modal utama menyelesaikan soal di atas adalah memahami konsep berikut ini.

Jika            y = f(x)
maka   f⁻¹(y) = x

Diketahui bahwa f(2x) = g(x − 3). Anggap saja keduanya sama dengan y.

y = f(2x)
y = g(x − 3)

Sekarang kita terapkan konsep di atas. Kita mulai dari fungsi yang kedua.

        y = g(x − 3)
g⁻¹(y) = x − 3
        x = g⁻¹(y) + 3 … (1)

Kita simpan dulu hasilnya. Kita lanjutkan menerapkan konsep di atas untuk fungsi yang pertama.

       y = f(2x)
f⁻¹(y) = 2x        … (2)

Selanjutnya kita substitusikan persamaan (1) ke persamaan (2).

f⁻¹(y) = 2[g⁻¹(y) + 3]
f⁻¹(y) = 2g⁻¹(y) + 6

Dengan menggantikan y dengan x diperoleh:

f⁻¹(x) = 2g⁻¹(x) + 6

Jadi, invers fungsi f adalah 2g⁻¹(x) + 6 (E).

Soal No. 54 tentang Matriks

Jika

maka det⁡ (P) = ….

A.   −3
B.   −2
C.   1
D.   2
E.   3

Pembahasan

Misalkan:

Sekarang kita terapkan data di atas untuk persamaan matriks yang pertama.

Diperoleh:

b = 1
d = 0

Dengan cara yang sama, persamaan matriks yang kedua menjadi:

Diperoleh:

a + b = −1
a + 1 = −1
      a = −2

c + d = 3
c + 0 = 3
      c = 3

Sehingga:

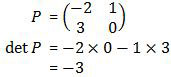
Jadi, determinan matriks P adalah 3 (A).

Soal No. 55 tentang Barisan dan Deret

Misalkan U_k dan S_k berturut-turut menyatakan suku ke-k dan jumlah k suku pertama suatu barisan aritmetika. Jika U₂ + U₄ + U₆ + U₈ + U₁₀ + U₁₂ = 72 maka S₁₃ = ….A.   81
B.   144
C.   156
D.   194
E.   312

Pembahasan

Cara 1

Rumus suku ke-k deret aritmetika dinyatakan

U_k = a + (k − 1)b

Berdasarkan rumus di atas maka:

U₂ = a + b
U₄ = a + 3b 
dan seterusnya

Dengan demikian,

U₂ + U₄ + U₆ + U₈ + U₁₀ + U₁₂ = 72
(a + b) + (a + 3b) + ⋯ + (a + 11b) = 72
6a + 36b = 72
    a + 6b = 12 … (1)

Sedangkan jumlah k suku pertama dirumuskan:

S_k = 1/2 k [2a + (k − 1)b]

Sehingga jumlah 13 suku pertama adalah:

S₁₃ = 1/2 × 13(2a + 12b)
S₁₃ = 13(a + 6b)              … (2)

Substitusi persamaan (1) ke persamaan (2) diperoleh:

S₁₃ = 13 × 12
S₁₃ = 156

Cara 2

Jumlah n suku barisan aritmetika yang berjarak tetap sama dengan perkalian antara banyak suku dan suku tengahnya (U_t).

S_n = n × U_t

Perhatikan penjumlahan suku yang tersaji pada soal di atas.

U₂ + U₄ + U₆ + U₈ + U₁₀ + U₁₂ = 72

Banyak suku yang dijumlahkan ada 6. Sedangkan suku tengah antara U₂ dan U₁₂ adalah U₇. Sehingga penjumlahan suku di atas menjadi:

6 × U₇ = 72
      U₇ = 12

Sekarang perhatikan pertanyaannya, yaitu S₁₃! Banyak suku yang dijumlah ada 13 sedangkan suku tengah antara U₁ dan U₁₃ adalah U₇. Sehingga:

S₁₃ = 13 × U₇
      = 13 × 12
      = 156

Jadi, jumlah 13 suku pertama barisan aritmetika tersebut adalah 156 (C).

Bagikan Artikel ini