Pembahasan Matematika Dasar No. 56 - 60 TKPA SBMPTN 2016 Kode Naskah 321

Pembahasan soal Matematika Dasar Tes Kemampuan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2016 kode naskah 321 nomor 56 sampai dengan nomor 60 tentang:

• geometri, 
• statistika, 
• limit fungsi, 
• sistem persamaan linear, dan 
• pertidaksamaan.

Soal No. 56 tentang Geometri

Titik X, Y, dan Z terletak pada segitiga ABC sehingga AZ = AY, BZ = BX, CX = CY seperti tampak pada gambar.

Jika BC, CA, dan AB berturut-turut adalah a cm, b cm, dan c cm, maka 2AY = … cm.A.   a + b + c
B.   a − b + c
C.   a + b − c
D.   −a − b + c
E.   b + c − a

Pembahasan

Perhatikan gambar berikut ini!

Misalkan:

AY = AZ = x

maka:

BX = BZ = c − x
CX = CA = b − x

Perhatikan sisi BC!

BC = BX + CX
   a = c − x + b − x
   a = b + c − 2x
 2x = b + c − a

Ingat, x = AY. Sehingga:

2AY = b + c − a

Jadi, nilai dari 2AY adalah b + c − a (E).

Soal No. 57 tentang Statistika

Seorang siswa mengikuti 6 kali ujian dengan nilai 5 ujian pertama adalah 6, 4, 8, 5, dan 7. Jika semua nilai dinyatakan dalam bilangan asli yang tidak lebih besar dari 10 dan rata-rata 6 kali ujian lebih kecil dari mediannya maka nilai ujian terakhir yang mungkin ada sebanyak ….A.   2
B.   3
C.   4
D.   6
E.   8

Pembahasan

Median adalah nilai tengah dari data yang telah diurutkan.

Perhatikan nilai 5 ujian yang telah diurutkan berikut ini:

4, 5, 6, 7, 8

Median dari 5 data tersebut adalah 6.

Misalkan nilai ujian ke-6 adalah x. Jika x adalah 1 sampai dengan 5 maka dapat diurutkan sebagai berikut:

x, 4, 5, 6, 7, 8

Median dari 6 data tersebut berada di antara 5 dan 6, yaitu 5,5.

Sementara itu, ketentuan pada soal adalah bahwa rata-rata dari 6 ujian lebih kecil dari mediannya.

Sedangkan jika x adalah 7 sampai 10 maka dapat diurutkan sebagai berikut:

4, 5, 6, 7, 8, x

Median dari ke-6 data tersebut berada di antara 6 dan 7, yaitu 6,5.

Nilai x yang mungkin bila rata-ratanya kurang dari median adalah:

Dengan demikian, nilai ulangan terakhir yang mungkin adalah:

1, 2, 7, atau 8 (ada 4 nilai)

Jadi, nilai ujian ke-6 yang mungkin ada sebanyak 4 (D).

Soal No. 58 tentang Limit Fungsi

Diketahui f(x) = x² + ax + b.
Jika f(b + 1) = 0 dan

maka a + 2b = ….A.   −2
B.   −1
C.   0
D.   1
E.   2

Pembahasan

Perhatikan limit fungsi yang tersaji pada soal!

Karena limit fungsi tersebut hasilnya ada, yaitu −1, maka dapat diterapkan aturan L’Hopital, yaitu pembilang dan penyebutnya masing-masing diturunkan.

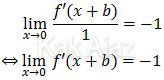
Sekarang perhatikan fungsi f.

       f(x) = x² + ax + b
      f'(x) = 2x + a
f'(x + b) = 2(x + b) + a
              = 2x + 2b + a

Nah, hasil f'(x + b) ini kita substitusikan ke limit di atas.

lim_x→0⁡ f'(x + b) = −1
lim_x→0⁡ 2x + 2b + a = −1

Dengan memasukkan x = 0 diperoleh:

2b + a = −1
a + 2b = −1

Jadi, nilai dari a + 2b adalah −1 (B).

Soal No. 59 tentang Sistem Persamaan Linear

Jika 3x − 2y = −1, −2x + 3y = 4, 4x + by = 4b, dan ax + 3y = 2a, maka a + b = ….A.   8
B.   4
C.   3
D.   −4
E.   −3

Pembahasan

Diketahui sistem persamaan linear:

3x − 2y = −1 … (1)
−2x + 3y = 4 … (2)
4x + by = 4b … (3)
ax + 3y = 2a … (4)

Eliminasi persamaan (1) dan (2)

  3x − 2y = −1 |×2|   6x − 4y = −2
−2x + 3y = 4   |×3| −6x + 9y = 12
                           ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  +
                                         5y = 10
                                           y = 2

Substitusi y = 2 ke persamaan (1).

3x − 4 = −1
      3x = 3
        x = 1

Selanjutnya kita substitusikan x = 1 dan y = 2 ke persamaan (3) dan (4).

4x + by = 4b
  4 + 2b = 4b
          4 = 2b
          b = 2

ax + 3y = 2a
    a + 6 = 2a
           a = 6

Dengan demikian:

a + b = 6 + 2
         = 8

Jadi, nilai dari a + b adalah 8 (A).

Soal No. 60 tentang Pertidaksamaan

Semua bilangan real x yang memenuhi

adalah ….A.   x < 0
B.   0 < x ≤ 2
C.   0 < x < 4
D.   2 ≤ x < 4
E.   x > 4

Pembahasan

Perhatikan pertidaksamaan berikut ini!

Pada pertidaksamaan di atas terdapat fungsi harga mutlak yang bentuknya sama, yaitu |x − 2|.

Fungsi yang terdapat dalam harga mutlak tersebut bernilai nol dan positif bila x ≥ 2 dan bernilai negatif bila x < 2.

I.   |x − 2| = x − 2    untuk x ≥ 2
II.  |x − 2| = −x + 2  untuk x < 2

Mari kita terapkan dua ketentuan tersebut untuk menyelesaikan pertidaksamaan di atas.

I.   Untuk x ≥ 2

Diperoleh: 2 ≤ x≤ 4

Karena syarat penyebut x ≠ 4 maka:

2 ≤ x < 4     ... (1)

II.  Untuk x < 2

Diperoleh: 0 ≤x ≤ 2

Karena syarat penyebut x ≠ 0 maka:

0 < x ≤2       …(2)

Penyelesaian akhir pertidaksamaan tersebut merupakan gabungan antara pertidaksamaan (1) dan (2). Diperoleh:

0 < x < 4

Jadi, bilangan real x yang memenuhi adalah 0 < x < 4 (C).

Bagikan Artikel ini