Pembahasan Matematika IPA UN 2017 No. 16 - 20

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 16 sampai dengan nomor 20 tentang:

• pertumbuhan dan peluruhan, 
• barisan dan deret geometri, 
• barisan dan deret aritmetika, 
• limit fungsi (mendekati tak hingga), serta 
• limit fungsi (bentuk pecahan akar).

Soal No. 16 tentang Pertumbuhan dan Peluruhan

Sebuah unsur radioaktif meluruh menjadi setengahnya dalam waktu 30 menit. Jika pada mulanya massa unsur tersebut 20 gram, massa unsur yang meluruh selama 2 jam adalah ….

A.   1,25 gram
B.   2,50 gram
C.   10,00 gram
D.   17,50 gram
E.   18,75 gram

Pembahasan

Peluruhan adalah berkurangnya suatu nilai dengan faktor pembagi yang tetap dalam setiap periode. Peluruhan dirumuskan sebagai:

L_n = L₀ (1 − r)ⁿ

dengan

L_n : sisa setelah meluruh n periode
L₀ : awal peluruhan
r   : faktor pembagi
n   : periode peluruhan

Sementara itu diketahui pada soal:

L₀ = 20 gram
r = 1/2

Peluruhan terjadi setiap 30 menit, berarti selama 2 jam (120 menit) periode peluruhannya adalah:

n = 120/30 = 4

Sisa unsur radioaktif tersebut setelah meluruh 2 jam adalah:

L_n = L₀ (1 − r)ⁿ
     = 20(1 − 1/2)⁴
     = 20 × (1/2)⁴
     = 20 × 1/16
     = 1,25

Dengan demikian, massa unsur yang meluruh adalah:

L₀ − L_n = 20 − 1,25
             = 18,75

Jadi, massa unsur yang meluruh selama 2 jam adalah 18,75 gram (E).

Soal No. 17 tentang Barisan dan Deret Geometri

Suku kedua dan kelima suatu barisan geometri adalah 3 dan 81. Jumlah n suku pertama barisan tersebut adalah ….

A.   3ⁿ⁺¹ − 3
B.   3ⁿ⁺¹ − 1
C.   2 ∙ 3ⁿ − 1
D.   1/2 (3ⁿ − 1)
E.   1/3 (3ⁿ − 1)

Pembahasan

Diketahui:

U₂ = 3
U₅ = 81

Rasio barisan geometri tersebut adalah:

Suku pertama bisa dicari melalui suku kedua.

U₂ = ar
   3 = a ∙ 3
   a = 1

Jumlah n suku pertama deret geometri dengan rasio lebih dari 1 dirumuskan sebagai:

Jadi, jumlah n suku pertama barisan tersebut adalah opsi (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 18 tentang Barisan dan Deret Aritmetika

Seutas tali dipotong menjadi 7 bagian dan masing-masing potongan membentuk deret aritmetika. Bila potongan tali terpendek adalah 6 cm dan yang terpanjang 384 cm, panjang tali semula adalah ….

A.   1.375 cm
B.   1.365 cm
C.   1.265 cm
D.   1.245 cm
E.   762 cm

Pembahasan

Diketahui:

n = 7
a = 6 cm
U₇ = 384 cm

Panjang tali semula adalah panjang tali sebelum dipotong menjadi 7 atau sama dengan jumlah ke-7 potongan tersebut.

S_n = n/2 (a + U_n)
S₇ = 7/2 (a + U₇)
     = 7/2 (6 + 384)
     = 7/2 ∙ 90
     = 1365

Jadi, panjang tali semula adalah 1.365 cm (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Barisan dan Deret.

Soal No. 19 tentang Limit Fungsi (mendekati tak hingga)

Nilai

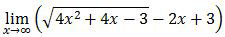
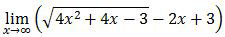
adalah ….A.   −4
B.   −2
C.   0
D.   2
E.   4

Pembahasan

Bentuk baku dari limit fungsi di atas adalah:

Nah, tugas kita adalah mengupayakan agar limit pada soal di atas berbentuk baku. Prinsipnya cukup sederhana.

Mari kita selesaikan dengan prinsip tersebut.

Bentuk di atas sudah baku. Berdasarkan bentuk baku tersebut diperoleh:

a = 4
b = 4 
d = −12

Dengan demikian, hasil dari limit fungsi di atas adalah:

Jadi, nilai dari limit fungsi tersebut adalah 4 (E).

Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi.

Soal No. 20 tentang Limit Fungsi (bentuk pecahan akar)

Nilai

adalah ….A.   −1/2
B.   −1/8
C.   1/8
D.   1/4
E.   1/2

Pembahasan

Limit fungsi berbentuk pecahan yang mengandung akar adalah dapat diselesaikan dengan mengalikan bilangan sekawan.

Pembilang berbentuk (a − b)(a + b) yang dapat disederhanakan menjadi a² − b². Sementara itu, penyebutnya berbentuk kuadrat yang dapat difaktorkan.

Pembilangnya harus kita upayakan agar saling meniadakan dengan salah faktor dari penyebut.

4 − (x + 2) = 4 − x − 2
                  = −x + 2
                  = −(x − 2)

Sehingga limit fungsi di atas bisa dilanjutkan menjadi:

Nah, ini bentuk terakhir dari limit tersebut. Sekarang kita substitusikan x = 2.

Jadi, nilai limit fungsi tersebut adalah 1/8 (C).

Bagikan Artikel ini