Pembahasan Matematika IPA UN 2017 No. 21 - 25

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPA nomor 21 sampai dengan nomor 25 tentang:

• aplikasi turunan [gradien], 
• aplikasi turunan [nilai maksimum], 
• integral substitusi, 
• integral tentu, serta 
• aturan sinus dan kosinus.

Soal No. 21 tentang Aplikasi Turunan [gradien]

Diketahui grafik fungsi y = 2x² − 3x + 7 berpotongan dengan garis y = 4x + 1. Salah satu persamaan garis singgung yang melalui titik potong kurva dan garis tersebut adalah ….

A.   y = 5x + 7
B.   y = 5x − 1
C.   y = x + 5
D.   y = 3x − 7
E.   y = 3x + 5

Pembahasan

Grafik fungsi kurva berpotongan dengan garis. Berarti di titik potong tersebut nilai dari keduanya adalah sama.

             y_kurva = y_garis
   2x² − 3x + 7 = 4x + 1
   2x² − 7x + 6 = 0
(2x − 3)(x − 2) = 0
x₁ = 3/2   atau   x₂ = 2

Kedua nilai absis di atas kita substitusikan ke fungsi kurva atau garis untuk mendapatkan nilai ordinatnya. (kita pilih fungsi garis karena lebih sederhana).

                       y = 4x + 1

x₁ = 3 /2  →  y₁ = 4 ∙ 3/2 + 1 = 7
x₂ = 2      →  y₂ = 4 ∙ 2 + 1 = 9

Sehingga titik potong kurva dan garis tersebut adalah:

(3/2, 7)    dan   (2, 9)

Kedua titik potong tersebut akan bertindak sebagai titik singgung.

Selanjutnya kita tentukan gradien garis singgung. Gradien merupakan turunan dari fungsi kurva y = 2x² − 3x + 7.

                        m = y'
                            = 4x − 3

x₁ = 3/2   →  m₁  = 4 ∙ 3/2 − 3 = 3
x₂ = 2      →  m₂  = 4 ∙ 2 − 3 = 5

Dengan demikian, persamaan garis singgungnya adalah:

y − y₁ = m₁ (x − x₁)
 y − 7 = 3(x − 3/2)
 y − 7 = 3x − 9/2
       y = 3x + 5/2

atau

y − y₂ = m₂ (x − x₂)
 y − 9 = 5(x − 2)
 y − 9 = 5x − 10
       y = 5x − 1

Jadi, sesuai opsi jawaban yang ada, salah satu persamaan garis singgung tersebut adalah y = 5x − 1 (B).

Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Integral.

Soal No. 22 tentang Aplikasi Turunan [nilai maksimum]

Sebuah akuarium tanpa tutup memiliki alas berbentuk persegi panjang dengan perbandingan panjang dan lebarnya 2 : 3. Jika luas permukaan akuarium adalah 1.800 cm², volume maksimum akuarium tersebut adalah ….

A.   3.600 cm³
B.   5.400 cm³
C.   6.300 cm³
D.   7.200 cm³
E.   8.100 cm³

Pembahasan

Diketahui:

l/p = 2/3 → l = 2/3 p
L = 1.800 cm²

Perhatikan sketsa akuarium berikut!

Luas akuarium tanpa tutup dirumuskan sebagai:

L = pl + 2pt + 2lt

Kita masukkan data luas dan substitusi l = 2/3 p pada rumus luas tersebut.

Sementara itu, volume akuarium dirumuskan:

V = p ∙ l ∙ t

Nah, sekarang kita jadikan rumus volume tersebut menjadi satu variabel, misal hanya terdiri dari variabel p.

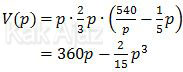
Volume akan maksimum bila turunan fungsi volume sama dengan nol.

            V'(p) = 0
360 − 2/5 p² = 0
          2/5 p² = 360
                p² = 360 ∙ 5/2
                     = 900
                  p = ±30

Dengan demikian, volume akuarium akan maksimum bila panjangnya 30 cm.

  V(p) = 360p − 2/15 p³
V(30) = 360 ∙ 30 − 2/15 ∙ 30³
          = 10800 − 3600
          = 7200

Jadi, volume maksimum akuarium tersebut adalah 7.200 cm³ (D).

Perdalam materi ini di Pembahasan Matematika UN: Aplikasi Integral.

Soal No. 23 tentang Integral Substitusi

Hasil dari

adalah ….

Pembahasan

Integral di atas adalah integral substitusi. Cirinya, pangkat tertinggi di dalam dan di luar akar berselisih 1.

Langkah pertama, ganti fungsi akar menjadi pangkat kemudian letakkan sebaris (tidak lagi berbentuk pecahan.

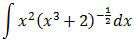
Selanjutnya, ganti dx dengan d(x³ + 2) kemudian bagi dengan turunannya.

Nah, sekarang kita tinggal mengintegralkan seperti biasanya, sebagaimana kita melakukan integral.

Jadi, hasil dari integral substitusi tersebut adalah opsi (C).

Perdalam materi ini di Pembahasan Matematika UN: Integral Fungsi Aljabar.

Soal No. 24 tentang Integral Tentu

Nilai

adalah ….A.   16
B.   20
C.   22
D.   32
E.   38

Pembahasan

Dikatakan integral tentu karena integral tersebut akan menghasilkan nilai tertentu, tidak mengandung konstanta integrasi (C).

Jadi, nilai dari integral tentu di atas adalah 16 (A).

Perdalam materi ini di Pembahasan Matematika UN: Integral Fungsi Aljabar.

Soal No. 25 tentang Aturan Sinus dan Kosinus

Sebuah kapal berlayar dari pelabuhan A ke pelabuhan B dengan jurusan tiga angka 080° sejauh 60 km. Kemudian berlayar menuju ke pelabuhan C dengan jurusan 200° sejauh 80 km.

Jarak antara pelabuhan C dan A adalah ….

A.   10 km
B.   5√13 km
C.   10√13 km
D.   20√13 km
E.   100 km

Pembahasan

Perhatikan rute perjalanan kapal berikut ini!

Berdasarkan gambar di atas, jarak CA dapat dicari dengan aturan kosinus berikut ini.

AC² = AB² + BC² − 2 AC ∙ BC cos⁡ B
        = 60² + 80² − 2 ∙ 60 ∙ 80 cos 60°
        = 3600 + 6400 − 9600 ∙ 0,5
        = 5.200
 AC = √5.200
        = 20√13

Jadi, jarak antara pelabuhan C dan A adalah 20√13 km (D).

Bagikan Artikel ini