Pembahasan Matematika IPS UN 2017 No. 1 - 5

Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 1 sampai dengan nomor 5 tentang:

• eksponen (bilangan berpangkat), 
• bentuk akar, 
• bentuk logaritma, 
• komposisi fungsi, dan 
• invers fungsi.

Soal No. 1 tentang Eksponen (bilangan berpangkat)

Diketahui x ≠ 0 dan y ≠ 0, bentuk sederhana

adalah ….

Pembahasan

Langkah pertama, 2/8 kita sederhanakan menjadi 1/4 yang jika dikuadratkan akan menghasilkan 1/16. Dengan langkah awal ini, opsi A, B, dan E sudah pasti salah.

Selanjutnya, variabel berpangkat negatif kita pindah agar berpangkat positif. x⁻⁵ kita pindah ke bawah sehingga menjadi x⁵. Sedangkan y⁻² kita pindah ke atas sehingga menjadi y².

Setelah itu, pangkat dari x dan y kita jumlahkan. Kemudian hasilnya kita kuadratkan.

Jadi, nilai dari bilangan berpangkat tersebut adalah opsi (C).

Soal No. 2 tentang Bentuk Akar

Bentuk sederhana dari √75 + 2√3 − √12 + √27 adalah ….A.   2√3
B.   5√3
C.   8√3
D.   12√3
E.   34√3

Pembahasan

Perhatikan kelima opsi jawaban yang disajikan. Semuanya mengandung akar 3. Oleh karena itu, kita ubah angka pada soal di atas sedemikian hingga mengandung angka 3. Misal 75 = 25 × 3.

   √75 + 2√3 − √12 + √27
= √(25∙3) + 2√3 − √(4∙3) + √(9∙3)

Nah, bilangan dalam akar selain 3 adalah bilangan kuadrat bukan? Tentunya bilangan tersebut bisa dikeluarkan dari akar. Mari kita selesaikan!

= 5√3 + 2√3 − 2√3 + 3√3
= (5 + 2 − 2 + 3)√3
= 8√3

Jadi, bentuk sederhana dari bentuk akar tersebut adalah 8√3 (C).

Soal No. 3 tentang Bentuk Logaritma

Nilai ⁷log ⁡4 ∙ ²log⁡5 + ⁷log⁡ (49/25) = ….

A.   1
B.   2
C.   3
D.   4
E.   5

Pembahasan

Bilangan yang bisa dijadikan bilangan berpangkat kita ubah terlebih dahulu.

4 = 2²
49/25 = (7/5)²

Sehingga soal di atas menjadi:

    ⁷log ⁡4 ∙ ²log⁡5 + ⁷log⁡ (49/25)
= ⁷log ⁡2² ∙ ²log⁡5 + ⁷log⁡ (7/5)²

Selanjutnya kita gunakan rumus ^alog⁡ bⁿ = n ^alog⁡ b.

= 2 ⁷log ⁡2 ∙ ²log⁡5 + 2 ⁷log⁡ (7/5)

Suku yang pertama kita selesaikan dengan rumus ^alog⁡ b ∙ ^blog⁡ c = ^alog⁡ c . Sehingga:

= 2 ⁷log⁡ 5 + 2 ⁷log⁡ (7/5)
= 2[⁷log⁡ 5 + ⁷log⁡ (7/5)]

Karena bentuk logaritma di atas mempunyai bilangan pokok yang sama, yaitu 7, maka dapat kita gunakan rumus ^alog⁡ b + ^alog⁡ c = ^alog⁡ bc.

= 2 ⁷log⁡ 5.(7/5)
= 2 ⁷log⁡ 7
= 2

Jadi, nilai dari bentuk logaritma di atas adalah 2 (B).

Soal No. 4 tentang Komposisi Fungsi

Diketahui fungsi f(x) = x² + 5x − 15 dan fungsi g(x) = x + 2. Fungsi komposisi (f ∘ g)(x) = ….A.   x² + 9x + 7
B.   x² + 9x − 1
C.   x² + 7x + 7
D.   x² + 5x + 7
E.   x² + 5x − 1

Pembahasan

Fungsi f(x) berarti fungsi f yang dinyatakan dalam x. Sedangkan fungsi (f ∘ g)(x) atau f[g(x)] adalah fungsi f yang dinyatakan dalam g(x).

    f(x) = x² + 5x − 15
f[g(x)] = [g(x)]² + 5g(x) − 15

Sekarang kita substitusikan g(x) = x + 2.

f[g(x) ] = (x + 2)² + 5(x + 2) − 15
             = x² + 4x + 4 + 5x + 10 − 15
             = x² + 9x − 1

Jadi, fungsi komposisi (f ∘ g)(x) adalah x² + 9x − 1 (B).

Soal No. 5 tentang Invers Fungsi

Fungsi f ∶ R → R didefinisikan

Invers dari f(x) adalah f⁻¹(x) = ….

Pembahasan

Invers fungsi bentuk pecahan linear dirumuskan sebagai:

Agar dapat memanfaatkan rumus di atas, kita ubah dulu penyebut dari fungsi f(x).

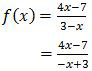
Dengan bentuk di atas, maka diperoleh a = 4, b = −7, c = −1, dan d = 3. Sehingga invers fungsi tersebut adalah:

Ternyata hasil di atas tidak ada pada opsi jawaban. Coba pembilang dan penyebutnya masing-masing dikalikan −1.

Jadi, invers dari fungsi f(x) adalah opsi (D).

Bagikan Artikel ini