Pembahasan Matematika IPS UN 2017 No. 26 - 30
Jumat, 25 Mei 2018
Tambah Komentar
Pembahasan soal-soal Ujian Nasional (UN) tahun 2017 bidang studi Matematika SMA-IPS nomor 26 sampai dengan nomor 30 tentang:
- integral tak tentu fungsi aljabar,
- integral tentu fungsi aljabar,
- jarak titik ke bidang pada ruang dimensi tiga,
- sudut antara dua garis dalam ruang dimensi tiga, dan
- trigonometri segitiga.
Soal No. 26 tentang Integral Tak Tentu Fungsi Aljabar
Hasil dari ∫ (10x4 − 6x2 − 4x) dx adalah ….
A. 40x3 − 12x − 4 + C
B. 5x5 − 3x3 − 2x2 + C
C. 2x5 − 2x3 − 2x2 + C
D. 2x5 + 3x3 − 2x2 + C
E. 2x5 − 3x3 − 4x2 + C
B. 5x5 − 3x3 − 2x2 + C
C. 2x5 − 2x3 − 2x2 + C
D. 2x5 + 3x3 − 2x2 + C
E. 2x5 − 3x3 − 4x2 + C
Pembahasan
Integral tak tentu fungsi aljabar dirumuskan sebagai:

Berdasarkan rumus di atas maka:
∫ (10x4 − 6x2 − 4x) dx
= 10 ∙ 1/5 x5 − 6 ∙ 1/3 x3 − 4 ∙ 1/2 x2 + C
= 2x5 − 2x3 − 2x2 + C
= 10 ∙ 1/5 x5 − 6 ∙ 1/3 x3 − 4 ∙ 1/2 x2 + C
= 2x5 − 2x3 − 2x2 + C
Jadi, hasil integral tak tentu fungsi aljabar di atas adalah opsi (C).
Soal No. 27 tentang Integral Tentu Fungsi Aljabar
Hasil dari

adalah ….A. 103
B. 76
C. 62
D. 40
E. 26

adalah ….A. 103
B. 76
C. 62
D. 40
E. 26
Pembahasan
Integral adalah integral yang menghasilkan nilai tertentu (tidak
mengandung konstanta integrasi C). Integral ini ditandai dengan batas
integrasi sehingga disebut juga dengan integral batas.
Integral tentu dirumuskan sebagai:
Mari kita selesaikan soal integral tentu tersebut dengan rumus di atas!

Jadi, hasil dari integral tentu fungsi aljabar tersebut adalah 76 (B).
Soal No. 28 tentang Jarak Titik ke Bidang pada Ruang Dimensi Tiga
Diketahui kubus ABCD.EFGH seperti pada gambar berikut.

Jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis ….A. AC
B. AD
C. AH
D. AF
E. AG

Jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis ….A. AC
B. AD
C. AH
D. AF
E. AG
Pembahasan
Jarak garis ke bidang adalah jarak tegak lurus antara garis dan bidang tersebut. Perhatikan gambar berikut!

Berdasarkan gambar di atas, dari titik A ke bidang CDHG hanya garis AD yang tegak lurus bidang CDHG.
Jadi, jarak titik A ke bidang CDHG dapat dinyatakan sebagai panjang ruas garis AD (B).
Soal No. 29 tentang Sudut antara Dua Garis dalam Ruang Dimensi Tiga
Diketahui limas beraturan T.ABCD dengan rusuk alas 6 cm dan rusuk tegak 6√2 cm.

Jika antara garis OT dan AT membentuk sudut λ, besar sudut λ adalah ….A. 0°
B. 30°
C. 45°
D. 60°
E. 90°

Jika antara garis OT dan AT membentuk sudut λ, besar sudut λ adalah ….A. 0°
B. 30°
C. 45°
D. 60°
E. 90°
Pembahasan
Garis OT dan AT bertemu di titik T. berarti sudut antara kedua titik tersebut terletak di titik T.
Perhatikan gambar berikut!
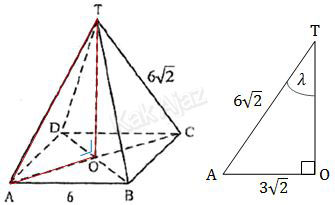
AO adalah setengah diagonal AC (diagonal bidang).
AO = 1/2 AC
= 1/2 × rusuk × √2
= 1/2 ×6 × √2
= 3√2
= 1/2 × rusuk × √2
= 1/2 ×6 × √2
= 3√2
Karena sisi pada segitiga AOT yang sudah kita ketahui adalah
‘demi’ (sisi depan sudut dan sisi miring) maka untuk menentukan sudut λ
kita gunakan rumus sinus.

Jadi, besar sudut antara garis OT dan AT adalah 30° (B).
Soal No. 30 tentang Trigonometri Segitiga
Diketahui ∆KLM siku-siku di M dan tan L= 1/3 √3. Nilai cos L adalah ….A. 1/2 √2
B. 1/2 √3
C. 1/2
D. √2
E. √3
B. 1/2 √3
C. 1/2
D. √2
E. √3
Pembahasan
Perhatikan ∆KLM dengan tan L = 1/3 √3 berikut ini!

Berdasarkan gambar di atas, sisi miring KL dapat dicari dengan rumus Pythagoras sebagai berikut:
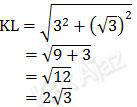
Dengan demikian, nilai dari kosinus sudut L adalah:

Jadi, nilai cos L adalah 1/2 √3 (B).



Belum ada Komentar untuk "Pembahasan Matematika IPS UN 2017 No. 26 - 30"
Posting Komentar