Pembahasan Matematika No. 6 - 10 TKD Saintek SBMPTN 2017 Kode Naskah 157

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 Kode Naskah 157 nomor 6 sampai dengan nomor 10 tentang:

• irisan kerucut, 
• suku banyak, 
• geometri, 
• integral, dan 
• limit fungsi trigonometri.

Soal No. 6 tentang Irisan Kerucut

Lingkaran x² + y² − 4x + 2y = 4 menyinggung hiperbola

Jika asimtot hiperbola tersebut mempunyai gradien 2 maka nila b² − a² = ….

A.   3
B.   6
C.   9
D.   12
E.   27

Pembahasan

Kita perhatikan persamaan lingkaran dan bentuk umumnya terlebih dahulu.

x² + y² − 4x + 2y − 4 = 0
x² + y² + Ax + By + C = 0

Dengan membandingkan bentuk umumnya, diperoleh:

A = −4
B = 2
C = −4

Pusat dan jari-jari lingkaran tersebut adalah:

pusat = (−½ A, −½ B)
         = (2, −1)

Jari-jari = √[¼ (A² + B²) − C]
            = √(¼ [(−4)² + 2²] − (−4))
            = √9
            = 3

Sekarang kita perhatikan persamaan hiperbola dan bentuk bakunya.

Berdasarkan persamaan baku tersebut, diperoleh:

Pusat = (h, k)
         = (2, −1)

Ternyata lingkaran dan hiperbola mempunyai titik pusat yang sama, yaitu (2, −1). Keadaan ini dapat digambarkan sebagai berikut:

Karena hiperbola menyinggung lingkaran maka puncak hiperbola tersebut adalah (−1, −1) dan (5, −1) (lihat gambar).

Mari kita substitusikan salah satu puncak tersebut ke persamaan hiperbola, ambil saja puncak (−1, −1).

Diketahui bahwa gradien asimtot hiperbola adalah 2, sehingga:

   b/a = 2
b²/a² = 4
  b²/9 = 4
     b² = 36

Dengan demikian,

b² − a² = 36 − 9
            = 27

Jadi, nila dari b² − a² adalah 27 (E).

Soal No. 7 tentang Suku Banyak

Jika p(x) = (x − 1)q(x) + 1 dan q(3) = 5 maka sisa pembagian p(x) oleh (x − 1)(x − 3) adalah ….

A.   2x − 1
B.   3x − 2
C.   5x − 4
D.   −3x + 4
E.   −5x + 6

Pembahasan

Untuk menyelesaikan soal di atas, kita pahami kembali teorema sisa berikut ini:

Jika f(x) dibagi x − a maka sisanya adalah f(a)

Karena yang ditanyakan sisa pembagian p(x) oleh (x − 1)(x − 3) maka kita tentukan dulu sisa pembagian oleh (x − 1) dan (x − 3), yaitu p(1) dan p(3).

p(x) = (x − 1)q(x) + 1

p(1) = (1 − 1)q(1) + 1
        = 0 + 1
        = 1

p(3) = (3 − 1)q(3) + 1
        = 2×5 + 1  [ingat q(3) = 5]
        = 11

Misalkan sisa pembagian p(x) oleh (x − 1)(x − 3) adalah p(x) = ax + b, maka:

p(1) = a + b = 1        … (1)
p(3) = 3a + b =11      … (2)
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  − [bawah dikurangi atas]
                 2a = 10
                   a = 5

Substitusi a = 5 ke persamaan (1).

5 + b = 1
      b = 4

Dengan demikian sisa pembagian tersebut adalah:

ax + b = 5x − 4
Jadi, sisa pembagian p(x) oleh (x − 1)(x − 3) adalah 5x − 4 (C).

Soal No. 8 tentang Geometri

Diketahui suatu lingkaran kecil dengan radius 3√2 melalui pusat suatu lingkaran besar yang mempunyai radius 6. Ruas garis yang menghubungkan dua titik potong lingkaran merupakan diameter lingkaran kecil, lihat gambar.

Luas daerah irisan kedua lingkaran adalah ….A.   18π + 18
B.   18π − 18
C.   14π + 14
D.   14π − 15
E.   10π + 10

Pembahasan

Perhatikan daerah irisan kedua lingkaran tersebut!

Daerah irisan kedua lingkaran tersebut terdiri dari dua daerah, yaitu daerah I dan II.

Daerah I merupakan luas setengah lingkaran kecil yang berjari-jari r_I = 3√2.

L_I = ½ × πr_I²
    = ½ × π × (3√2)²
    = 9π

Sedangkan daerah II merupakan tembereng dari lingkaran besar.

Tali busur AB merupakan diameter lingkaran kecil sehingga ∠AOB = 90°.

Luas daerah II merupakan pengurangan dari luas juring AOB dengan luas segitiga AOB.

L_II = L_j.AOB − L.∆AOB
     = (90°/360°) × πr_II² − 1/2 × r_II²
     = 1/4 × π × 6² − 1/2 × 6²
     = 9π − 18

Dengan demikian, luas daerah irisan kedua lingkaran tersebut adalah:

L = L_I + L_II
   = 9π + 9π − 18
   = 18π − 18

Jadi, luas daerah irisan kedua lingkaran adalah 18π − 18 (B).

Soal No. 9 tentang Integral

Jika

dengan f(x) fungsi genap dan

maka

A.   0
B.   1
C.   2
D.   3
E.   4

Pembahasan

Mari kita pahami terlebih dahulu perbedaan antara fungsi genap dan fungsi ganjil!

Fungsi Genap

Jika f(x) fungsi genap maka berlaku:

• f(−a) = f(a)
• grafik f(x) dalam interval −a ≤ x ≤ a berbentuk simetris

Fungsi Ganjil

Jika f(x) fungsi ganjil maka berlaku:

• f(−a) = −f(a)
• grafik f(x) dalam interval -a ≤ x ≤ a berlawanan tanda

Nah, mari kita selesaikan soal di atas!

f(x) adalah fungsi genap dan sin ⁡x adalah fungsi ganjil sehingga f(x) sin ⁡x adalah fungsi ganjil.

Dengan demikian diperoleh:

Selanjutnya kita tuntaskan integral berikut ini.

Jadi, nilai dari integral fungsi f(x) dengan batas −2 sampai dengan 0 adalah 0 (A).

Soal No. 10 tentang Limit Fungsi Trigonometri

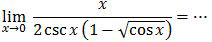
A.   −2
B.   −1
C.   0
D.   1
E.   2

Pembahasan

Langkah pertama kita ubah csc⁡ x menjadi 1/sin ⁡x.

Kemudian kita kalikan dengan bilangan sekawan dari 1 − √(cos⁡ x), yaitu 1 + √(cos⁡ x).

Analogi dari rumus cos⁡ 2x = 1 − 2 sin²⁡x, diperoleh cos⁡ x = 1 − 2 sin²⁡ ½x sehingga 1 − cos⁡ x = 2 sin²⁡ ½x.

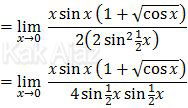
Limit trigonometri mendekati nol berlaku sin⁡ x = x sehingga:

Nah, sekarang tinggal memasukkan x = 0.

= 1 + √(cos ⁡0 )
= 1 + 1
= 2

Jadi, nilai limit fungsi trigonometri tersebut adalah 2 (E).

Bagikan Artikel ini