Pembahasan Matematika SMP UN 2017 No. 21 - 25

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2017 nomor 21 sampai dengan nomor 25 tentang:

• unsur-unsur lingkaran, 
• sudut pusat dan sudut keliling lingkaran, 
• juring lingkaran, 
• garis dan sudut, serta 
• luas bangun datar.

Soal No. 21 tentang Unsur-unsur Lingkaran

Perhatikan gambar lingkaran dengan pusat O!

Garis AB adalah ….

A.   busur
B.   jari-jari
C.   apotema
D.   tali busur

Pembahasan

Berikut ini adalah keterangan untuk gambar pada soal di atas.

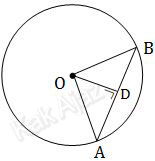
Keterangan:

• Jari-jari adalah garis dari titik pusat ke keliling lingkaran: garis OA atau garis OB
• Tali busur adalah garis lurus yang menghubungkan dua titik pada lingkaran: garis AB
• Busur adalah garis lengkung yang menghubung-kan dua titik pada lingkaran: lengkung AB
• Apotema adalah garis yang ditarik dari titik pusat tegak lurus tali busur: garis OD

Jadi, garis AB pada lingkaran di atas adalah tali busur (D).

Soal No. 22 tentang Sudut Pusat dan Sudut Keliling Lingkaran

Perhatikan gambar lingkaran berpusat O berikut!

Besar ∠AOB = 110°, besar ∠BDC = ….A.   80°
B.   70°
C.   55°
D.   35°

Pembahasan

∠AOB berpelurus dengan ∠BOC sehingga:

∠AOB + ∠BOC = 180°
    110° + ∠BOC = 180°
                ∠BOC = 180° − 110°
                ∠BOC = 70°

Sedangkan ∠BOC merupakan sudut pusat dari sudut keliling ∠BDC. Besar sudut pusat sama dengan dua kali besar sudut keliling.

∠BOC = 2 × ∠BDC
     70° = 2 × ∠BDC
∠BDC = 35°

Jadi, besar ∠BDC pada lingkaran tersebut adalah 35° (D).

Soal No. 23 tentang Juring Lingkaran

Sebuah taman berbentuk juring lingkaran dengan panjang jari-jari 21 m dan sudut pusat 120°. Pada sekeliling taman akan dipasang pagar kawat 2 kali putaran. Minimal panjang kawat yang diperlukan adalah ….A.   44 meter
B.   64 meter
C.   86 meter
D.   172 meter

Pembahasan

Sebuah taman berbentuk juring lingkaran dengan panjang jari-jari 21 m dan sudut pusat 120°.

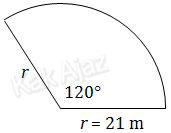
Panjang busur lingkaran taman adalah:

Keliling taman tersebut adalah:

K = 2 × r + busur
    = 2 × 21 + 44
    = 86

Sedangkan pagar taman tersebut adalah kawat 2 kali putaran sehingga:

panjang kawat = 2 × K
                        = 2 × 86
                        = 172

Jadi, panjang minimal kawat yang diperlukan adalah 172 meter (D).

Soal No. 24 tentang Garis dan Sudut

Perhatikan gambar!

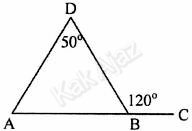
Besar ∠BAD adalah ….A.   50°
B.   60°
C.   70°
D.   80°

Pembahasan

∠BAD berpelurus dengan ∠ABD sehingga:

∠BAD + ∠ABD = 180°
    120° + ∠ABD = 180°
                ∠ABD = 60°

Sedangkan jumlah sudut-sudut segitiga adalah 180°.

∠BAD + ∠ABD + ∠ADB = 180°
           ∠BAD + 60° + 50° = 180°
                   ∠BAD + 110° = 180°
                               ∠BAD = 70°

Jadi, besar ∠BAD pada gambar di atas adalah 70° (C).

Soal No. 25 tentang Luas Bangun Datar

Lantai gedung pertunjukan yang berukuran 25 m × 15 m akan dipasangi ubin berukuran 50 cm × 50 cm. Banyak ubin yang diperlukan adalah ….A.   1.500 ubin
B.   1.200 ubin
C.   150 ubin
D.   100 ubin

Pembahasan

Luas lantai gedung pertunjukan adalah:

L_g = 25 × 15 m²
     = 375 m²
     = 3.750.000 cm²

Sedangkan luas sebuah ubin adalah:

L_u = 50 × 50 cm²
     = 2.500 cm²

Dengan demikian, banyak ubin yang diperlukan adalah:

Jadi, banyak ubin yang diperlukan adalah 1500 ubin (A).

Bagikan Artikel ini